An Overview of MOD Function | Microsoft Excel
Microsoft Excel, a powerhouse in data analysis, boasts an array of functions catering to diverse mathematical needs. Among these, the MOD function stands tall as a versatile tool for handling remainders in numeric calculations. In this article, we will delve into the intricacies of the MOD function in Excel, unveiling its syntax, applications, and how it enhances accuracy in numerical computations within spreadsheets. The MOD function is one of the math and trigonometry functions in Microsoft Excel. It can be used as a standalone function and in collaboration with other functions. This article will give you an overview of the MOD function in Excel.
What is MOD Function in Excel?
The MOD function calculates the remainder when a numerical value (dividend) is divided by another one (divisor).
Syntax for MOD function,
=MOD(number, divisor)Here,
- number: Compulsory. It refers to the dividend i.e. the number to divide.
- divisor: Compulsory. The number by which you want to divide the dividend.
This will return a numerical value i.e. the remainder.
Examples of MOD Function
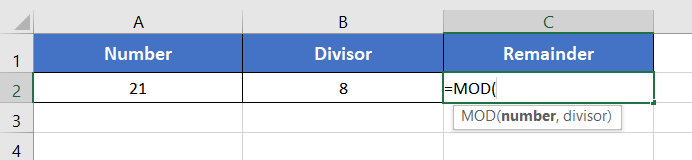
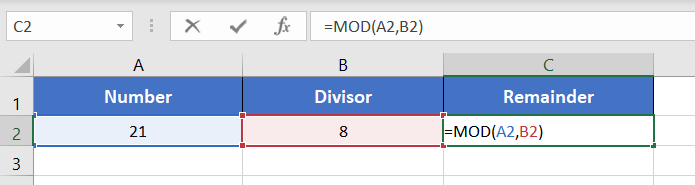
Suppose, you have the number 39 in cell A2. Then you have a divisor 5 in cell B2. Let’s say you want to calculate the remainder if you divide 39 by 5. Well, you can use the MOD function to get the remainder quite easily. For that, use the formula:
=MOD(A2,B2)The output will be 4.
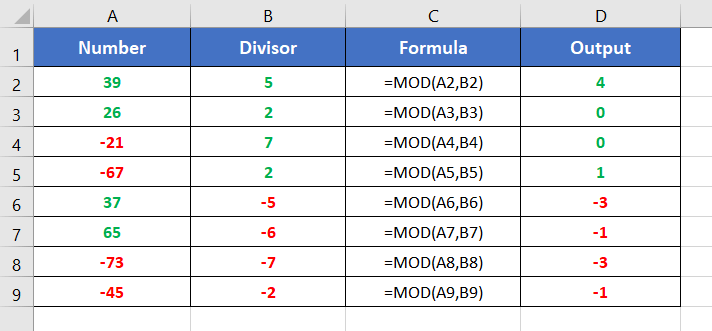
Here are some examples of the usage of the MOD function.
Procedure to Use the MOD Function
Using the MOD function in Excel involves a straightforward procedure. The MOD function calculates the remainder when one number is divided by another. Here’s a step-by-step guide:
- Start with inserting an equal sign (=) in a blank cell.
- Then type MOD.
- Type open parenthesis “(“.
As you type the open parenthesis, Excel shows the syntax of the MOD function.
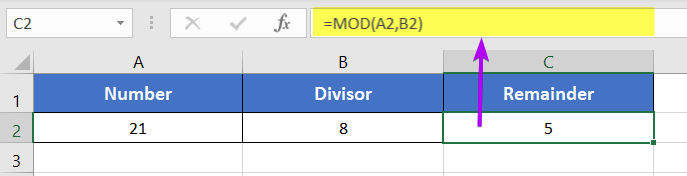
- Insert a number first.
You can directly insert a number or a cell address that contains a number.
Here, I’m inserting A2 which has the number 21. - Then insert a comma (,).
After inserting the comma, Excel will ask you for the second argument which is the divisor.
- Now insert the divisor.
You can insert the cell address of the divisor or directly insert a number as a divisor. Here, the divisor is in cell B2. So, I’m inserting B2 inside the function.
The MOD function returns 5. Because, when you divide 21 by 8, the remainder is 5. Thus, the output is 5.
Availability
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Remarks
- The MOD function shows #VALUE! error in the case of non-numeric values.
- The sign of the remainder is the same as the sign of the divisor. This means for the positive divisor, the remainder becomes positive. For a negative divisor, the remainder becomes negative.
Conclusion
The MOD function in Microsoft Excel proves to be a powerful asset for handling remainders in numeric calculations. Whether you’re dealing with cyclic patterns, time-sensitive data, or creating visually dynamic spreadsheets, understanding and incorporating the MOD function into your Excel toolkit enhances your ability to perform precise and tailored numerical computations. By leveraging MOD, you empower yourself to unravel the complexities of remainders and seamlessly integrate them into your data analysis workflow. The MOD function is one of the math and trigonometry functions in Excel. If you have any questions regarding the MOD function, please comment below. Thanks!
Frequently Asked Questions
What is the MOD row function in Excel?
In Excel, the MOD function can be employed with row numbers to create cyclic patterns or perform calculations based on row positions. The general syntax for using MOD with row numbers is as follows: =MOD(ROW() – start_row + 1, cycle_length)
- ROW(): Returns the current row number.
- start_row: Specifies the initial row from which the calculation begins.
- cycle_length: Defines the length of the cyclic pattern.
This formula calculates the remainder when the row number is adjusted by the starting row and divided by the cycle length. It’s commonly used in scenarios where you want to repeat a pattern every certain number of rows.
For example:=MOD(ROW() – 1, 3) + 1
This formula creates a cyclic pattern of 1, 2, 3, 1, 2, 3, and so on, for each row in the Excel sheet.
In summary, while there is no specific “MOD row function,” the MOD function can be effectively used with row numbers in Excel for various purposes, such as creating dynamic patterns or performing calculations based on the row position.
How to solve 4 mod 2?
The result of “4 mod 2” is 0. In modular arithmetic, the term MOD stands for the modulus operation, which calculates the remainder when one number is divided by another.
For “4 mod 2,” you divide 4 by 2, and the remainder is 0 because 4 is evenly divisible by 2. Therefore, the solution to “4 mod 2” is 0.